Anna OliveiraConfira a atividade de Matemática sobre ângulos em retas paralelas, transversais e em triângulos, elaborada para o 7º ano, com gabarito e alinhada à BNCC, tudo pronto para sala de aula.
O tema permite explorar propriedades fundamentais da geometria, como a relação entre ângulos formados por retas paralelas cortadas por uma transversal e a soma dos ângulos internos de um triângulo.
O objetivo desta atividade é desenvolver o raciocínio lógico e a capacidade de resolver problemas geométricos, estimulando a observação, a análise e a justificativa das respostas. Além disso, busca-se incentivar o uso de representações gráficas e fluxogramas, promovendo maior compreensão dos conceitos matemáticos e fortalecendo habilidades que serão aplicadas em estudos futuros de geometria e trigonometria.
Clique aqui para mais atividades de Matemática
Questões
1) Observe a figura abaixo com duas retas paralelas cortadas por uma transversal.
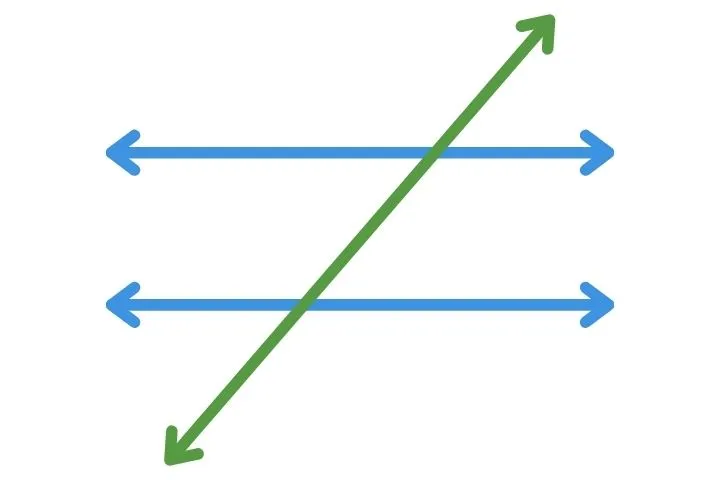
a) Identifique um par de ângulos alternos internos.
b) Identifique um par de ângulos correspondentes.
2) Se uma reta transversal forma um ângulo de 65° com uma das retas paralelas, qual será a medida do ângulo correspondente a ele?
3) Qual a medida do terceiro ângulo do triângulo abaixo?
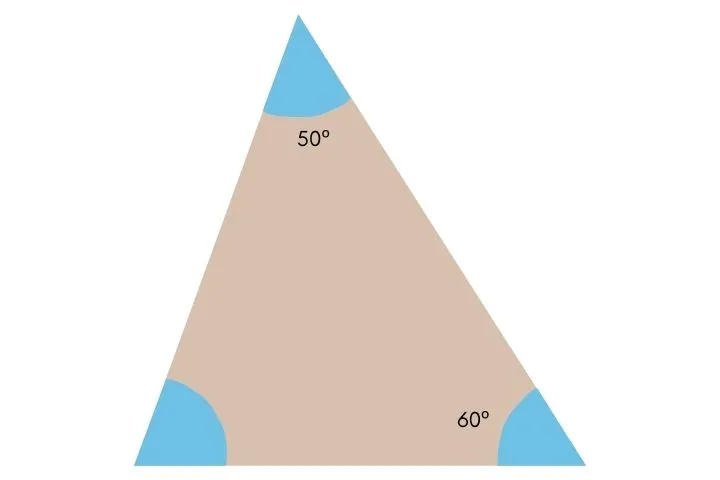
4) Explique, com suas palavras, por que os ângulos alternos internos em retas paralelas cortadas por uma transversal são sempre iguais.
5) Construa, com régua e compasso, um triângulo com lados de 5 cm, 6 cm e 7 cm.
a) É possível construir o triângulo?
b) Justifique sua resposta com a condição de existência de triângulos.
6) Em um fluxograma, organize os passos para descobrir a medida de um ângulo alterno interno quando já se conhece a medida do ângulo externo correspondente.
7) Uma transversal forma um ângulo de 120° com uma reta paralela. Qual será a medida do ângulo interno adjacente a ele?
8) Observe o triângulo abaixo. Se um dos ângulos agudos mede 37°, qual é a medida do outro ângulo agudo?
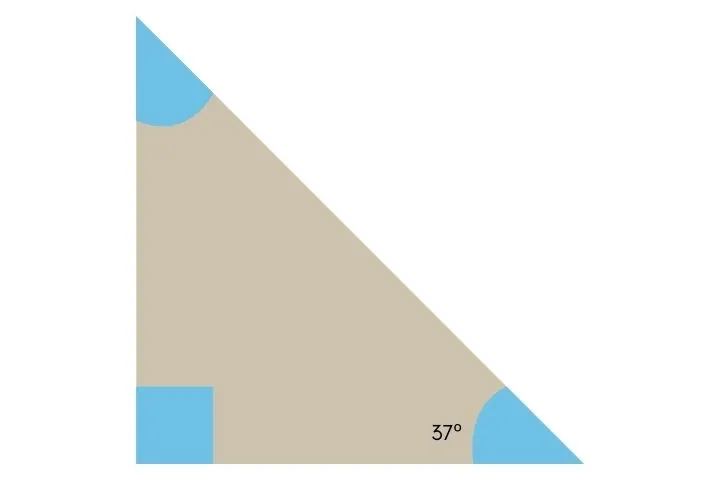
9) Duas retas paralelas são cortadas por uma transversal. O ângulo obtuso mede 110°.
a) Qual será a medida do ângulo agudo adjacente?
b) Qual será a medida de um ângulo alterno interno a esse ângulo obtuso?
10) Na figura abaixo, duas retas paralelas são cortadas por uma transversal.
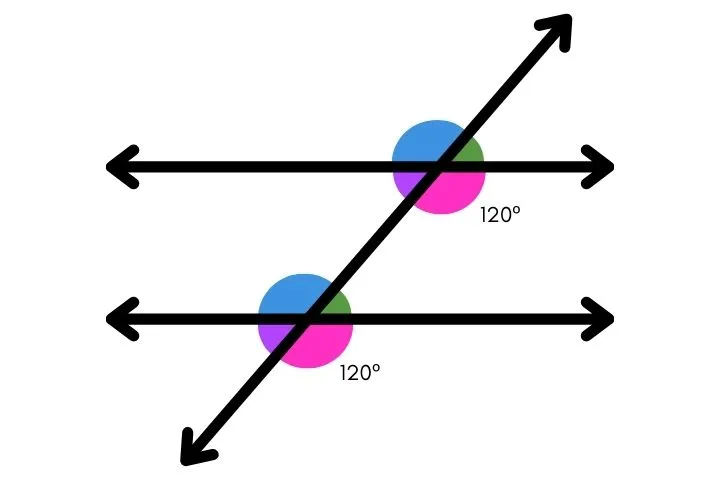
a) Qual é a medida do ângulo alterno interno correspondente?
b) Qual é a medida do ângulo suplementar a esse ângulo de 120°?
Habilidades trabalhadas
| Código | Descrição |
|---|---|
| EF07MA23 | Verificar relações entre os ângulos formados por retas paralelas cortadas por uma transversal, com e sem uso de softwares de geometria dinâmica. |
| EF07MA07 | Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas. |
| EF07MA24 | Construir triângulos, usando régua e compasso, reconhecer a condição de existência do triângulo quanto à medida dos lados e verificar que a soma dos ângulos internos de um triângulo é 180°. |
Gabarito da atividade de ângulos
Atividade 1:
a) Exemplo: ∠1 e ∠2 (alunos podem citar qualquer par correto de alternos internos).
b) Exemplo: ∠3 e ∠4 (qualquer par correto de correspondentes).
Atividade 2:
65°.
Atividade 3:
70°.
Atividade 4:
Porque, quando duas retas são paralelas, a transversal mantém a mesma inclinação em relação a ambas. Assim, os ângulos alternos internos ocupam posições iguais em relação às paralelas e, por isso, sempre têm a mesma medida.
Atividade 5:
a) Sim.
b) A soma de dois lados é maior que o terceiro, então o triângulo pode existir.
Atividade 6:
- Identificar ângulo externo.
- Calcular suplemento (180° – valor).
- Relacionar com o ângulo alterno interno.
Atividade 7:
60°.
Atividade 8:
53°.
Atividade 9:
a) 70°.
b) 110°.
Atividade 10:
a) 120°.
b) 60°.
