Confira a atividade sobre volume de prismas, elaborada especialmente para o Ensino Médio, com gabarito e alinhada à BNCC.
A proposta desta atividade é desenvolver a compreensão dos alunos sobre o cálculo do volume de prismas por meio de situações contextualizadas e desafios que envolvem não apenas fórmulas, mas também interpretação espacial, raciocínio lógico e aplicação prática.
Ao resolver problemas que abordam o empilhamento de objetos, o uso eficiente do espaço e a conversão de unidades de medida, os estudantes são estimulados a refletir sobre a utilidade da Matemática em contextos reais, como na organização de produtos, no armazenamento de materiais e na arquitetura.
Além disso, as questões incentivam a investigação dos princípios que fundamentam o cálculo de volumes, como o Princípio de Cavalieri, promovendo o pensamento crítico e a dedução de fórmulas de maneira ativa.
Clique aqui para mais atividades de Matemática
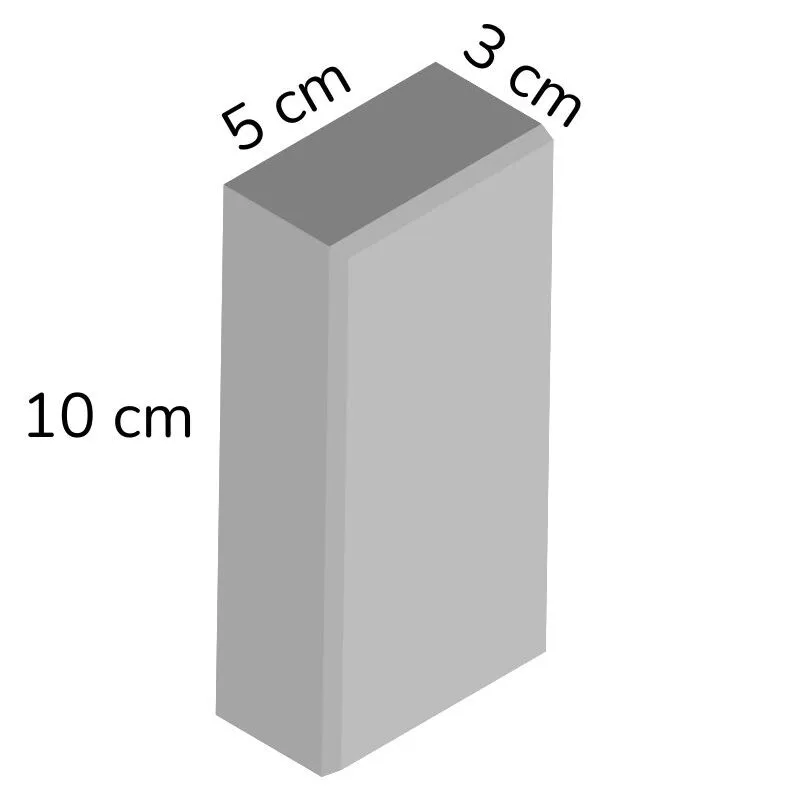
1) Um paralelepípedo tem base retangular com dimensões 5 cm por 3 cm e altura de 10 cm. Qual o seu volume?
a) 15 cm³
b) 30 cm³
c) 150 cm³
d) 180 cm³
2) Um compartimento em forma de prisma reto tem base retangular de 10 cm por 6 cm e altura de 36 cm. Dentro dele, serão colocadas pequenas caixas também em forma de prisma retangular, com base de 5 cm por 3 cm e altura de 6 cm. Considerando o empilhamento perfeito e sem folgas, quantas dessas caixas cabem dentro do compartimento?
a) 10
b) 12
c) 24
d) 36
3) Um reservatório em forma de prisma reto com base hexagonal regular possui 6 m² de área da base e altura de 5 m. Qual o volume do reservatório?
a) 11 m³
b) 15 m³
c) 30 m³
d) 60 m³
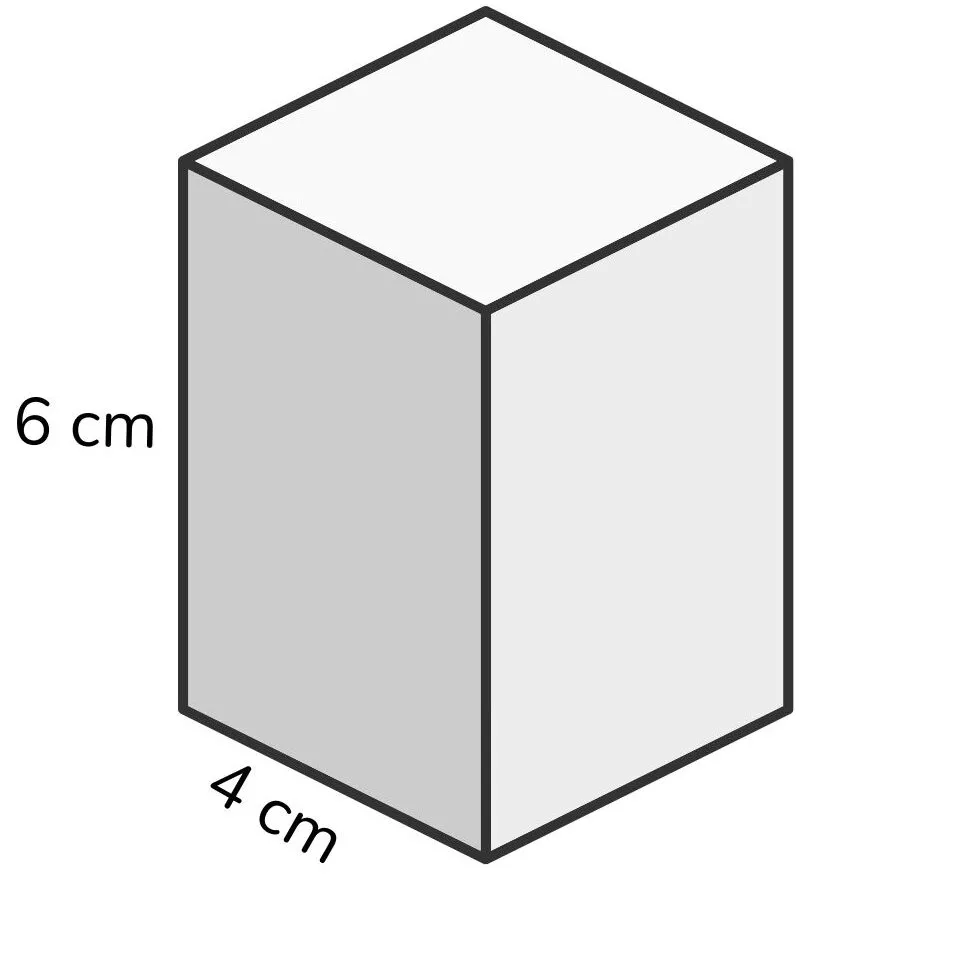
4) Dado um prisma com base quadrada de lado 4 cm e altura de 6 cm, o volume desse sólido é:
a) 24 cm³
b) 48 cm³
c) 96 cm³
d) 64 cm³
5) Um confeiteiro precisa organizar potes cilíndricos de glacê com 5 cm de diâmetro e 8 cm de altura, sempre empilhados na vertical, dentro de caixas organizadoras com tampa, em formato de paralelepípedo reto-retângulo. A ideia é colocar o máximo de potes possível em cada caixa, desde que todos estejam em pé, com tampa fechada, sem amassar os potes nem ultrapassar os limites da caixa.
No estoque da loja, ele encontra cinco modelos diferentes de caixas, todos pelo mesmo preço, conforme a tabela:
| Modelo | Comprimento (cm) | Largura (cm) | Altura (cm) |
| A | 20 | 10 | 16 |
| B | 25 | 15 | 12 |
| C | 30 | 10 | 24 |
| D | 18 | 18 | 20 |
| E | 24 | 12 | 16 |
Considerando o empilhamento perfeito dos potes com as tampas voltadas para cima, qual modelo permite armazenar o maior número de potes por caixa?
a) Modelo A
b) Modelo C
c) Modelo D
d) Modelo E
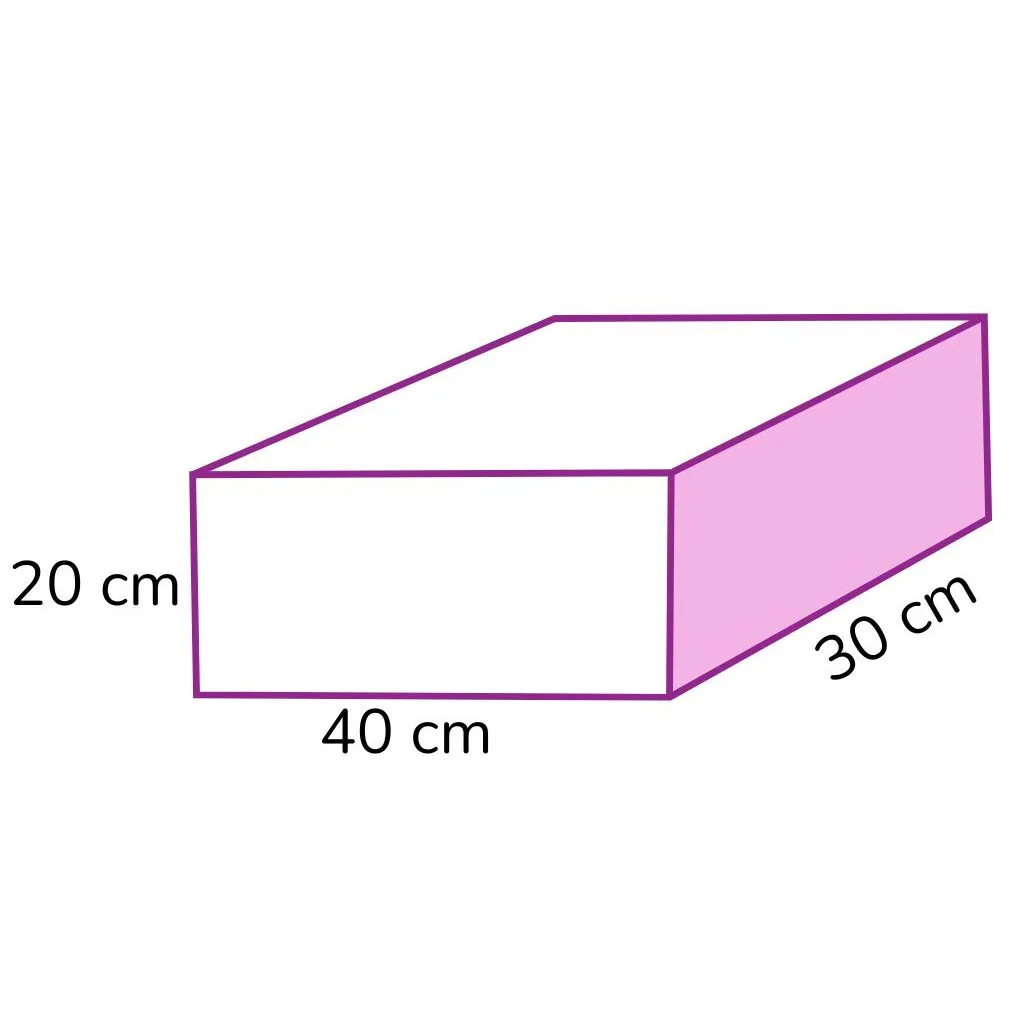
6) Uma caixa em forma de paralelepípedo tem dimensões internas de 40 cm de comprimento, 30 cm de largura e 20 cm de altura. Se cada embalagem de sabonete ocupa 240 cm³, quantas unidades cabem no máximo dentro da caixa, desconsiderando espaços vazios?
a) 50
b) 100
c) 150
d) 200
7) Uma caixa de papelão tem formato de paralelepípedo retângulo, com 50 cm de comprimento, 30 cm de largura e 40 cm de altura. O volume total da caixa é utilizado para armazenar um produto líquido, e o fabricante deseja saber quantos litros cabem nessa caixa, desconsiderando perdas.
a) 60 L
b) 75 L
c) 100 L
d) 120 L
8) O volume de um prisma regular com base pentagonal é 300 cm³ e sua altura é 10 cm. Qual é a área da base?
a) 30 cm²
b) 20 cm²
c) 15 cm²
d) 25 cm²
9) Uma embalagem prismática tem base retangular de 7 cm por 7 cm e altura de 20 cm. Qual seu volume?
a) 980 cm³
b) 490 cm³
c) 140 cm³
d) 1960 cm³
10) Um bloco em forma de prisma reto tem volume de 960 cm³ e área da base igual a 120 cm². Qual é a altura desse bloco?
a) 6 cm
b) 8 cm
c) 10 cm
d) 12 cm
Habilidades trabalhadas
| Código | Descrição |
|---|---|
| EM13MAT309 | Resolver e elaborar problemas que envolvem o cálculo de áreas totais e de volumes de prismas, pirâmides e corpos redondos em situações reais (como o cálculo do gasto de material para revestimento ou pinturas de objetos cujos formatos sejam composições dos sólidos estudados), com ou sem apoio de tecnologias digitais. |
| EM13MAT504 | Investigar processos de obtenção da medida do volume de prismas, pirâmides, cilindros e cones, incluindo o princípio de Cavalieri, para a obtenção das fórmulas de cálculo da medida do volume dessas figuras. |
| EM13MAT307 | Empregar diferentes métodos para a obtenção da medida da área de uma superfície (reconfigurações, aproximação por cortes etc.) e deduzir expressões de cálculo para aplicá-las em situações reais. |
Gabarito da atividade de volume de prismas
Este conteúdo te ajudou? Considere colaborar com o nosso site sendo um membro através de uma pequena doação:



