Confira atividade de seno, cosseno e tangente, ou seja, relações métricas em triângulos para resolver problemas em contextos geométricos e do cotidiano. O objetivo é desenvolver o raciocínio lógico, estimular a aplicação prática dos conceitos trigonométricos e aprofundar o conhecimento sobre as propriedades dos triângulos. A atividade é voltada para turmas de Matemática do Ensino Médio. Ao final, confira as habilidades da BNCC que regem a atividade e o gabarito.
Para mais atividades de matemática, clique aqui.
1) Um estudante quer calcular a largura de um rio. Ele marca dois pontos A e B na margem, separados por 80 m. Do ponto A, ele mede um ângulo de 60° em relação à linha AB, apontando para um ponto C na outra margem. Do ponto B, o ângulo em relação à linha AB para C é de 50°. Qual é a largura aproximada do rio (distância perpendicular até o ponto C)?
2) Em um triângulo ABC, os lados AB e AC medem 10 cm e 12 cm, respectivamente, e o ângulo entre eles mede 75°. Qual é o comprimento do lado BC?
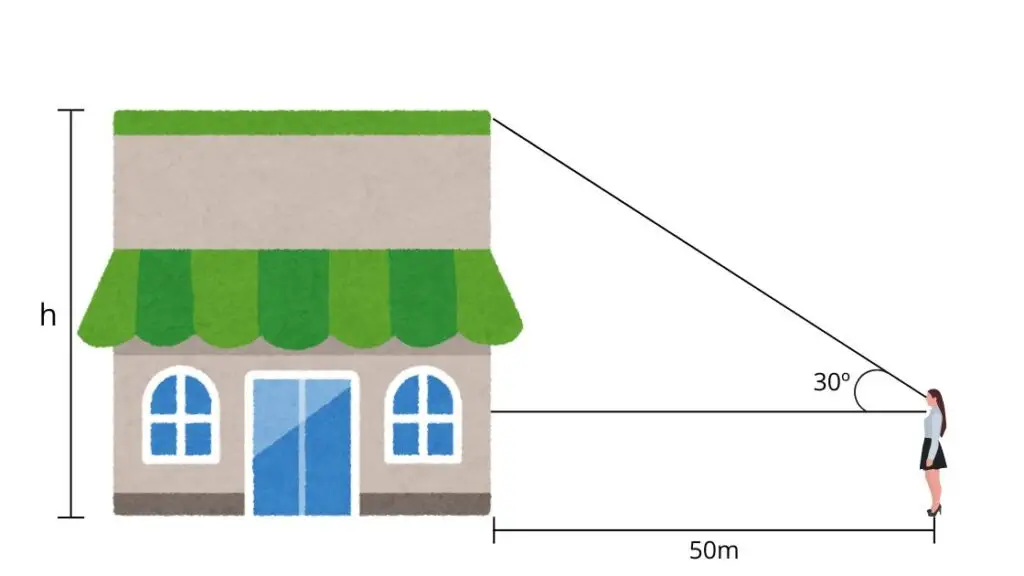
3) Uma pessoa observa o topo de um prédio a um ângulo de elevação de 30°, estando a 50 m da base. Qual é a altura aproximada do prédio?
4) Uma rampa tem 4 m de altura e 6 m de comprimento na base horizontal. Qual é o ângulo aproximado de inclinação da rampa em relação ao solo?
5) Em um triângulo, os lados medem 7 cm, 9 cm e o ângulo oposto ao lado de 7 cm é de 40°. Qual é a medida aproximada do ângulo oposto ao lado de 9 cm?
6) Uma árvore projeta uma sombra de 15 m. O ângulo de elevação do Sol nesse momento é de 45°. Qual é a altura aproximada da árvore?
7) De um ponto a 20 m de altura, observa-se um objeto no solo a um ângulo de depressão de 60°. Qual é a distância horizontal entre a base e o objeto?
8) Em um triângulo, dois lados medem 14 cm e 18 cm, e o ângulo entre eles é de 60°. Calcule o comprimento do terceiro lado.
9) Em um triângulo retângulo, o cateto oposto mede 5 cm e o adjacente 12 cm. Qual é a medida aproximada do ângulo formado entre o cateto adjacente e a hipotenusa?
10) De um ponto a 200 m da base de uma montanha, o ângulo de elevação até o topo é de 35°. Qual é a altura aproximada da montanha?
| Habilidades trabalhadas na atividade de seno, cosseno e tangente | Descrição |
|---|---|
| EM13MAT308 | Aplicar as relações métricas, incluindo as leis do seno e do cosseno ou as noções de congruência e semelhança, para resolver e elaborar problemas que envolvem triângulos, em variados contextos. |
| EM13MAT309 | Resolver e elaborar problemas que envolvem o cálculo de áreas totais e volumes, que podem incluir triângulos em contextos de superfícies ou sólidos. |
| EM13MAT307 | Empregar diferentes métodos para a obtenção de medidas de áreas (por exemplo, decompondo em triângulos). |
| EM13MAT314 | Resolver e elaborar problemas envolvendo grandezas determinadas por razão ou produto de outras, o que pode incluir razões trigonométricas (em alguns contextos). |
Gabarito da atividade de seno, cosseno e tangente
Atividade 1: Aproximadamente 65 metros.
Atividade 2: Aproximadamente 13,5 cm.
Atividade 3: Aproximadamente 28,9 metros.
Atividade 4: Aproximadamente 34°.
Atividade 5: Aproximadamente 56°.
Atividade 6: Aproximadamente 15 metros.
Atividade 7: Aproximadamente 11,5 metros.
Atividade 8: Aproximadamente 16,4 cm.
Atividade 9: Aproximadamente 23°.
Atividade 10: Aproximadamente 140 metros.