Confira atividade de funções polinomiais de 1º e 2º grau. A atividade tem como foco turmas de matemática do Ensino Médio. Ao final, confira as normas da BNCC que regem essa atividade e o gabarito.
Clique aqui para ver mais atividades de matemática.
1) Considere a função f(x)=3x−7.
a) Qual o valor de f(0)?
b) Qual o zero da função (valor de x tal que f(x)=0)?
2) Dadas as funções f(x)=5 e g(x)=x, responda:
a) Qual o gráfico de cada uma dessas funções?
b) Como se comportam essas funções quanto à taxa de variação?
3) A função h(x)=−2x+4 representa uma função polinomial do 1º grau.
a) Qual é a taxa de variação de h?
b) O gráfico dessa função é crescente ou decrescente? Justifique.
4) Observe o gráfico de uma função do 1º grau.
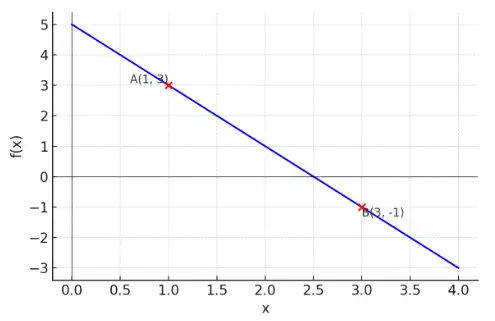
a) Determine a expressão algébrica da função, sabendo que ela passa pelos pontos A(1,3) e B(3,−1)
5) Duas funções do 1º grau são dadas por f(x)=x+2 e g(x)=−3x+1.
a) Qual a imagem de x=2 em cada função?
b) Compare a taxa de variação de ambas.
6) Considere a função quadrática f(x)=x²−4x+3.
a) Calcule as raízes da função.
b) Determine o vértice e classifique-o como ponto de máximo ou mínimo.
c) Esboce o gráfico da função.
7) A função f(x)=−2x²+8x−6 tem concavidade voltada para cima ou para baixo?
Justifique sua resposta com base no coeficiente de x².
Determine o intervalo em que a função é crescente e o intervalo em que ela é decrescente
8) Considere a função f(x)=x². A partir dela, indique o que acontece com o gráfico nas seguintes transformações:
a) g(x)=x²+3
b) h(x)=(x−2)
c) p(x)=−x²
9) A função f(x)=x²−6x+8 representa a trajetória de um objeto lançado.
a) Determine o ponto de máximo ou mínimo.
b) Em que intervalos a função está crescendo e decrescendo?
c) Qual o valor mínimo da função?
10) Dada a função f(x)=2x²+4x−6, calcule:
a) As raízes da função.
b) O valor de f(0).
c) O valor de x em que a função atinge seu valor mínimo.
d) A imagem da função no intervalo [−3,2].
| Habilidades trabalhadas na atividade de funções polinomiais de 1º e 2º grau | Descrição |
| EM13MAT501 | Investigar relações entre números expressos em tabelas para representá-los no plano cartesiano, identificando padrões e criando conjecturas para generalizar e expressar algebricamente essa generalização, reconhecendo quando essa representação é de função polinomial de 1º grau. |
| EM13MAT502 | Investigar relações entre números expressos em tabelas para representá-los no plano cartesiano, identificando padrões e criando conjecturas para generalizar e expressar algebricamente essa generalização, reconhecendo quando essa representação é de função polinomial de 2º grau do tipo y = ax2. |
| EM13MAT402 | Converter representações algébricas de funções polinomiais de 2º grau em representações geométricas no plano cartesiano, distinguindo os casos nos quais uma variável for diretamente proporcional ao quadrado da outra, recorrendo ou não a softwares ou aplicativos de álgebra e geometria dinâmica, entre outros materiais. |
Gabarito da atividade de funções polinomiais de 1º e 2º grau
Atividade 1:
f(x) = 3x – 7
a) f(0) = 3(0) – 7 = -7
b) 3x – 7 = 0 → x = 7/3
Atividade 2:
a) f(x) = 5: reta horizontal, paralela ao eixo x, passando por y = 5
g(x) = x: reta com 45°, passando pela origem
b) g(x) = x: taxa de variação = 1 (função identidade)
f(x) = 5: taxa de variação = 0 (função constante)
Atividade 3:
h(x) = -2x + 4
a) Taxa de variação = -2
b) A função é decrescente, pois o coeficiente de x é negativo.
Atividade 4:
a) Inclinação m = (-1 – 3)/(3 – 1) = -4/2 = -2
Usando a equação da reta: y = mx + b
3 = -2(1) + b → b = 5
Equação: f(x) = -2x + 5
b) A função é decrescente, pois o coeficiente angular é negativo.
Atividade 5:
f(x) = x + 2
g(x) = -3x + 1
a)f(2) = 2 + 2 = 4
g(2) = -3(2) + 1 = -6 + 1 = -5
b)g(x): taxa de variação = -3 (decrescente)
f(x): taxa de variação = 1 (crescente)
Atividade 6:
a) Raízes:
Δ = (-4)² – 4(1)(3) = 16 – 12 = 4
x = (4 ± 2)/2 → x = 1 ou x = 3
b) Vértice:
x_v = -(-4)/2(1) = 2
f(2) = 2² – 4(2) + 3 = 4 – 8 + 3 = -1
Vértice: (2, -1)
É ponto de mínimo, pois a > 0
Atividade 7:
a) Concavidade voltada para baixo (a = -2 < 0)
b) Vértice:
x_v = -8 / 2(-2) = -8 / -4 = 2
f(2) = -2(2²) + 8(2) – 6 = -8 + 16 – 6 = 2
Vértice: (2, 2)
Crescente no intervalo (-∞, 2)
Decrescente no intervalo (2, ∞)
Atividade 8:
a) g(x) = x² + 3 → translação para cima, 3 unidades
b) h(x) = (x – 2)² → translação para a direita, 2 unidades
c) p(x) = -x² → reflexão em relação ao eixo x (muda concavidade)
Atividade 9:
a) Vértice:
x_v = 6 / 2 = 3
f(3) = 3² – 6(3) + 8 = 9 – 18 + 8 = -1
Vértice: (3, -1)
b) Crescente: (3, ∞)
Decrescente: (-∞, 3)
c) Valor mínimo = -1
Atividade 10:
a) Raízes:
Δ = 4² – 4(2)(-6) = 16 + 48 = 64
x = (-4 ± 8)/4 → x = -3 ou x = 1
b) f(0) = -6
c) Vértice:
x_v = -4 / (2*2) = -1
f(-1) = 2(-1)² + 4(-1) – 6 = 2 – 4 – 6 = -8
Vértice: (-1, -8)
d) Imagem no intervalo [-3, 2]:
f(-3) = 2(9) + 4(-3) – 6 = 18 – 12 – 6 = 0
f(-2) = 8 – 8 – 6 = -6
f(-1) = -8
f(0) = -6
f(1) = 2 + 4 – 6 = 0
f(2) = 8 + 8 – 6 = 10
Variação da função no intervalo: de -8 até 10
Imagem: { -8, -6, 0, 10 }